Recall the formula for the period of a mass
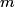 attached to a spring with spring constant attached to a spring with spring constant 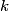 whose other side is attached to a wall: whose other side is attached to a wall: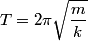 Also, recall that the effective spring constant of two springs in parallel is 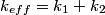 and the effective spring constant of two springs in series is and the effective spring constant of two springs in series is 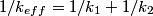 . So, the effective spring constant for Figure . So, the effective spring constant for Figure 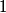 is is 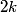 and the effective spring constant for Figure and the effective spring constant for Figure 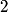 is is 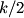 Therefore, the desired ratio is 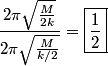 Therefore, answer (A) is correct. |